
 . I bet, this is the scene in your home too (if you are a lazy kid
. I bet, this is the scene in your home too (if you are a lazy kid  ) I never felt the importance of organizing things until I realized that searching of certain things becomes really difficult when you don’t arrange your things. Being a computer enthusiast, I wondered how such large amount of data was organized in computer
) I never felt the importance of organizing things until I realized that searching of certain things becomes really difficult when you don’t arrange your things. Being a computer enthusiast, I wondered how such large amount of data was organized in computer . Later I was enlightened(
. Later I was enlightened( ) by the amazing concept of Data Structures that binds everything together in an organized way.
) by the amazing concept of Data Structures that binds everything together in an organized way.
Coming to Data Structures, it is a particular way where in data is organized and stored so that it can be used efficiently. Array, Hash table, stacks, queues, binary heap, Linked Lists are few popular data structures. In this blog, we'll discuss another ingenious data structure known as Fibonacci Heaps.
Fibonacci heap!! Fibonacci series and Heaps !! Whoa..Two amazing concepts spliced together !! Michael L. Fredman and Robert E. Tarjan are the brains behind it.
Let us start the kindergarten of Fibonacci heap
Level 0: Pre- Requisites
In order to understand this, it’s good if you have a prior knowledge about the data structure circularly doubly linked list. If you can’t recall what it is,just take a look at the figure below.
- Inserting or removing a node from any location is done in O(1) time.
- Given two circularly doubly linked lists, we can concatenate them into one list in O(1) time.
Another basic concept of heap should be known.
Min-Heap : A heap in which the value of the parent node is less than that of the child nodes.
We are done with the pre-requisites. Just make sure that you are thorough with it.
Level 1: Structure of a node in Fibonacci heap.
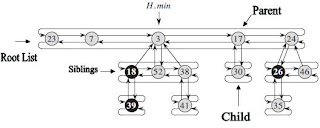
Siblings: Children of same node are called siblings. Obvious isn’t it? :)
Node label: Name of the node.
Key: Information that the node holds.
Degree: It is a attribute of a node to indicate the number of children it has.
Mark : It is a Boolean value which indicates if it has lost one of its child or not
Child: A pointer of a node that points to any one of its children.
Structure of a Fibonacci Heap:
- Fibonacci heap is a collection of many trees.
- Roots of such trees form the root list.
- H.min is a heap attribute that points to the minimum in the root list.
One important thing to be noted is that the values in the root list are unordered but the trees in the heap are min-heap ordered.
Level 3: Operations.
- MAKE-FIB-HEAP :
- INSERT (H, x) : H is the Heap. x is the node label.
- Finding the minimum node: Accessing the H.min gives the minimum.
- UNION (H1, H2):

- Extract-Minimum (H):
 But as the root list has to be optimized, CONSOLIDATE function is used to set everything right. It aims at having nodes in the root list with distinct degree in order to minimize the number of elements in the root list.
But as the root list has to be optimized, CONSOLIDATE function is used to set everything right. It aims at having nodes in the root list with distinct degree in order to minimize the number of elements in the root list.
- · Decrease Key (H, x, k):
1. Say a node G is marked and has a child P.
2. P has children X and Y.
3. As a result of some operation say P lost its child Y. Now P is marked and is left with the only child 'X'.
4. Lets say the node 'X' is decreased by a finite amount.
5. There are two possibilities.
a. H.min < X.key
b. X.key < H.min (Violation of the heap min-heap property)
6. What we know is that H.min has to be sheltered in root list and H.min is the minimum among all the other elements of heap. Hence we just CUT the node X and is attached as the left sibling of the H.min(again by convention).
7. Now due to Decrease-Key operation even X will have to part from P which means P is losing its second child. Unfair right?
8. Hence P is detached from G and attached as the left sibling of the H.min now. This detachment is termed as CASCADING CUT.
9. But what about G? G is marked and has already lost one of its child. To add to the sorrows, it losing P now. Hence G is detached from its parent and added into the root list as the left sibling of H.min.
10. This goes on till it encounters a node which is unmarked. These are called CASCADING CUTS which are recursive in nature.
- Delete Key:
Firstly decrease the key to -∞ and extract the minimum. The node gets deleted.
Why is this better?
‘A stitch in time saves nine’. This proverb stands as a backbone in all walks of life and so in computer science. The true usefulness of the data structure is decided based on the time it takes to perform certain operations on it.
Here we look at the amortized time it takes to perform all these operations. Clearly, Fibonacci heaps are way better when compared to the time complexity of the binomial heaps.
Why the name ‘Fibonacci’ heap?
We have come almost to the end of the story and still we haven’t justified the name given to it. Formally speaking,.
If Fk represents the kth Fibonacci number, then the size of a node x is always greater than Fk+2, where k is the degree of the node x.
Size(x) is nothing but the size of the tree rooted at x i.e. the number of nodes it holds including itself.

Let us take the example of this figure.
By the rule,
Hence this is a part of Fibonacci heap. Basically, the idea of Fibonacci series is plugged into the concept of heap and all together a new data structure called ‘Fibonacci Heap’ is formed.
If you did not understand any of the above, here is the essence of it. Fibonacci heap is a data structure which is desirable when the number of EXTRACT-MIN and DELETE operations is small relative to the number of other operations performed. It is an efficient data structure. It finds its application in Dijkstra's algorithm, Minimum Spanning Tree etc. For more details on this, please download
By the way, my Mom is a sweet lady and so am I









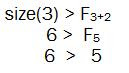

Didn't know so much about Fibonacci heaps . Never wondered why the name. Learnt a lot :)
ReplyDeleteThank you
The story that opens up ur blog, just great..:):)loved the way you related the need of organising things in real life with computer and the solution to it-data structures..:)
ReplyDeleteInterestingly written..:) dividing the concepts into levels and penning it down in point-wise fashion was an excellent system...makes the reader to wanna read it..;):)
Like u had said ‘A picture speaks a thousand words’ and 'yes' it did...Diagrams of heaps were useful for understanding..:):)
Very well explained, especially in situations like 'This function plays a role of a broker who bonds two heaps into one with minimum commission'..that was a great idea :):)
A few points should have been elaborated a bit more like 'consolidate function','cuts' ,'cascading cuts'..it kind of became very abstract..:)Otherwise very nicely explained..:):)
I did get to know the structure and operations on Fibonacci heap a lot better after reading this..:):)
The comic and yeah the use of smileys made it a visual treat..creative:):)..just like the start ,the ending was again 'great'...:)
Excellent start!! Funny and enjoyable :)
ReplyDeleteThe structure of fibonacci heap is neatly explained with the diagram and so are the operations.Just little confused in understanding decrease key operation.But could understand the whole process.
I still dint get the whole point of naming it fibonacci, but the explanation gave many ideas.
Very beautifully and nicely explained.
"Why is it better?", the idea of explaining with images is brilliant. Got the whole point when i saw the table.
Proper use of "smileys" has been made!! very colorful :) :)
Nice start:)Importance of data structures is well told.The figures in all the levels help in understanding.
ReplyDeleteAll the operations were easy to understand:)
The blog looks colourful overall.
"Later the heap is restructured to preserve its property by CUTS and CASCADING CUTS." hey what is cuts and cascading cuts?.
Everything said and done,makes a fabulous take on
fibonacci heaps:)
great blog,shruthi.
ReplyDeleteit looks like you are a "cormen" book fan too...
but casting the story,....communicating the essence and purpose of data structure with the dirty room thing was nice.
the superiority of the fibonacci heap to other data structures is well illustrated.
as far as i can see,
the fibonacci heap is an excellent DS to implement dictionary structures.
owing to its excellent data retrieval and organization time.
a very appropriate topic to write a blog on....the applications of this particular DS is wide and elegant.
long live tarjan!
and great work with the intro.
and
PS: i do agree with the fact that some terms like "cascading cuts" require a sight more explanation....
@all - Thank u :) I have attempted to explain CUTS and CASCADING CUTS. Please let me know if I am not clear.
ReplyDelete